http://www.cuentosinfin.com/ojos-de-perro-azul/

Matematica: Perimetro y Area

Perímetro y área

Perímetro: es la suma de los lados de una figura geométrica. Es su contorno.

Ejemplos:

Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm

10 cm

El perímetro del rectángulo lo obtenemos sumando todos sus lados:

Perímetro = 10 cm + 5 cm + 10 cm + 5 cm  = 30 cm

Por lo tanto, el perímetro del rectángulo es 30 cm.

Respecto al cuadrado , el perímetro (la longitud de su contorno) se obtiene sumando sus cuatro lados

En la figura, los lados del triángulo miden 4 m.

Para obtener el perímetro sumamos sus lados:

Perímetro = 4 m + 4 m + 4 m  = 12 m

El perímetro del triángulo es 12 m

Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.

Área de un rectángulo

El área del rectángulo corresponde a la medida de la región verde, y se obtiene multiplicando la base por la altura.

Área = base · altura

Ejemplo:

Los lados del rectángulo de la figura miden 10 cm. y 5 cm.

10 cm	La altura de este rectángulo mide 5 cm.
10 cm	La base de este rectángulo mide 10 cm.

Área = 10 · 5 = 50 cm 2

el área del rectángulo es 50 cm 2

El centímetro cuadrado (cm 2 ) es una unidad que nos permite medir áreas. También pueden ser metros cuadrados (m 2 ), milímetros cuadrados (mm 2 ), etc.

Área del cuadrado

El área de un cuadrado es igual al producto de lado por lado.

Área de un triángulo

El área de un triángulo es igual a la mitad de su base por la altura.

Ejemplos:

Si la base de un triángulo mide 10 cm y su altura mide 5 cm., entonces el área del triángulo es 25 cm 2

Cálculo del Área del Cuadrado y del Triángulo

Nos basamos en lo estudiado en el caso del rectángulo.
El cuadrado tiene sus cuatro lados iguales, lo que quiere decir que la largura y la anchura son iguales:

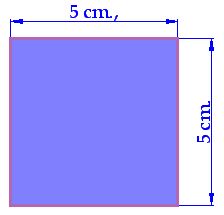
Para calcular el área del cuadrado tengo multiplicar el largo por el ancho, pero como valen lo mismo, multiplico por sí misma una de las medidas:

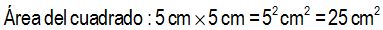
Comprobación:
Si cuentas los centímetros cuadrados verás que son 25:

15(2).10 ¿Cuál es el área de una pared cuyas medidas son 2 metros de longitud por 2 metros de altura?

Respuesta: 

CÁLCULO DEL ÁREA DEL TRIÁNGULO

Nos vamos a fijar en el rectángulo para saber como se calcula el área del triángulo.
En la figura siguiente tenemos un rectángulo que tiene 10 cm. de largo por 8 de ancho.
No pierdas de vista a la diagonal:

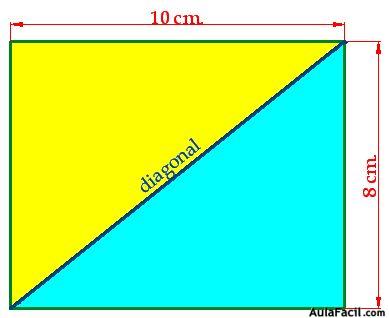
15(2).11 Dibuja en un papel un rectángulo con las medidas de la figura anterior y traza la diagonal. Recorta la figura y no la estropees que la vas a necesitar.

Observa la figura siguiente:

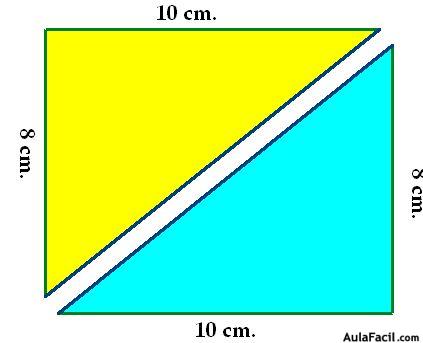
Hemos cogido las tijeras y hemos cortado por la diagonal y nos han quedado dos triángulos iguales.
Haz tu lo mismo, corta por la diagonal y tendrás en tus manos dos triángulos que tienen 10 cm., de largo por 8 centímetros de alto o de anchura máxima. Es mejor que hablemos de altura.
Antes de cortar por la diagonal, ¿cuál era el área del rectángulo?

Exactamente: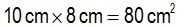 

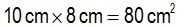
Como el rectángulo ha quedado dividido en dos partes iguales, cada una de ellas valdrá:

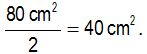
Cada una de las dos partes es un triángulo cuya superficie vale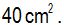 

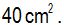
Para obtener esta cantidad, hemos multiplicado la base por la altura del rectángulo y luego hemos dividido por dos ya que los dos triángulos juntos valen el área del rectángulo.
Fíjate bien en los dos recortes que has obtenido al cortar el rectángulo por la diagonal. Tienes dos superficies triangulares que al juntarlas por la diagonal forman el rectángulo.

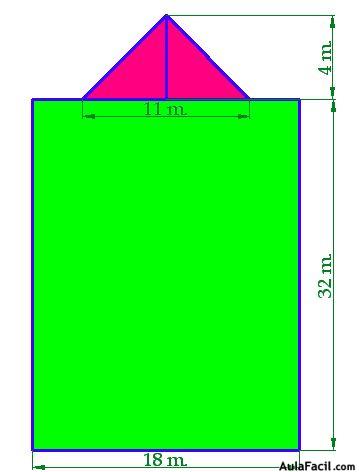
15(2).12 En la figura anterior tienes un dibujo que representa la fachada de una casa a la que hay que pintarla. Su figura geométrica la componen un triángulo y un rectángulo cuyas medidas las tienes indicadas.

Calcula el precio que cuesta pintarla si tenemos que pagar 1,65 € el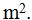 

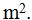
Respuesta: 986,70 €

Matemática: Tabla de valor posicional

TABLA DE VALOR POSICIONAL

Todo número tiene dos valores Valor por sí mismo: que es siempre el mismo valor esté donde esté colocada cada cifra.  Valor de posición: Es el valor que tiene cada cifra de acuerdo al lugar que ocupa en la cantidad. Observemos la tabla siguiente:    CENTENAS DECENAS UNIDADES 1 1 1 Esto me representa el número 111 = Ciento once  Busquemos los valores por sí mismo y el valor de posición del 111  Valor por sí mismo de 111 1 = 1 1 = 1 1 = 1 El valor por sí mismo es el valor que tiene cada número por su figura esté donde esté dentro de la cantidad. Valor de posición de 111 1 Centena = 100 Unidades 1 Decena = 10 Unidades 1 Unidad = 1 Unidad El valor de posición es el que tiene cada número de acuerdo a donde se encuentre ubicado dentro de la cantidad. Este lápiz representa 1 UNIDAD por lo tanto dentro de la tabla de posición el número 1 estará dentro de las UNIDADES así:    CENTENAS DECENAS UNIDADES     1 Esto quiere decir que tengo 2 UNIDADES  Por lo tanto coloco el 2 en la casilla de las unidades así:  CENTENAS DECENAS UNIDADES     2 8 lápices = 8 UNIDADES    CENTENAS DECENAS UNIDADES     8 ¿Cómo colocarías el número 13 dentro de la tabla de posición si cada casilla sólo acepta un número? Tenemos entonces que buscar con cuántas unidades se forma una DECENA   De las 13 UNIDADES que tengo selecciono 10 que me representan 1 DECENA las restantes UNIDADES las coloco en la casilla de las UNIDADES Entonces la representación del 13 en la tabla de posiciones quedaría así: CENTENAS DECENAS  UNIDADES   1 3 La representación de 23 en la tabla de posición será así:    CENTENAS DECENAS  UNIDADES   2 3 RESUMIENDO  Cuando tu mamá te manda a la panadería a comprar 5 panes, estás comprando 5 UNIDADES de pan.   Pero si en lugar de 5 panes te manda a comprar 34 panes, entonces estás comprando 34 UNIDADES de pan; lo que es lo mismo 3 DECENAS de pan (una decena son diez unidades) más 4 UNIDADES de pan.  Ahora debes estar listo para representar el 34 en la tabla de posición.     CENTENAS DECENAS UNIDADES Ejercicios Coloca dentro de la tabla de posición cada una de las cantidades que aparecen a continuación:     CENTENAS DECENAS UNIDADES Así: 394 3 9 4 19 450 259   Diga cuántas DECENAS se pueden formar con cada una de las unidades siguientes:       DECENAS UNIDADES ASI: 57= 5 7 99 20 85